La division avec la pascaline

L'exemple donné dans "Usage de la machine" pour la division reprend les mêmes nombres que ceux utilisés pour la multiplication. Soit à diviser 23688 par 56 On se place en position soustraction et après avoir initialisé la machine on fait apparaître le dividende à l'afficheur. On écrit le diviseur sur une bande de papier en espaçant les chiffres d'une distance égale à celle qu'il y a entre les lucarnes. La bande de papier se place du côté gauche entre les roues étoilées et les lucarnes d'affichage.

Avant de traiter l'exemple proposé, le manuscrit expose le principe de l'opération en quelques lignes. Il faut trouver :

"[...] Mais comme il pourrait arriver que l'on mette un chiffre trop grand au quotient en prenant ainsi toujours le premier chiffre du diviseur pour sa valeur juste, je le prends toujours pour un de plus qu'il ne vaut [...] Ensuite je me sers de ce quotient pour multiplier le diviseur, après avoir mis sur la machine les chiffres que me donne cette multiplication je trouve aux fenêtres des tambours ce qui reste à diviser. Que si ce restant est encore plus grand que le diviseur c'est une marque que le quotient devait être plus fort, mais ce ne sera jamais que d'1 et l'on ajoutera cet 1 au-dessous du quotient qu'on aura marqué."

Donc avec notre exemple de 437 divisé par 23, on regarde combien de fois 2+1 est contenu dans 4, la réponse est 1. Lorsqu'on retranche 1 fois 23 de 43 il reste 20 qui est plus petit que 23 donc le premier chiffre du quotient est bien égal à 1.

Si l'on avait divisé 475 par 23, le même raisonnement aurait conduit à retrancher 23 de 47. Dans ce cas il reste 24 qui est plus grand que 23, il est donc possible de retrancher 23 une fois de plus. Le premier chiffre du quotient n'est donc pas 1 mais 2.

Reprenons le manuscrit :

" [...] Je mets donc sur cette bande 56 pour l'exemple proposé et en posant ces chiffres au-dessous des deux premiers à gauche du dividende qui font 23, je vois que ce nombre 56 excède celui de 23 et par conséquent que je ne puis opérer sur ces deux nombres, puisque 56 n'est pas contenu une seule fois en 23, ce qui m'oblige d'avancer cette bande à droite en sorte que les chiffres 5 et 6 répondent sous le second et le troisième chiffre du dividende [...] et alors je suis en état de chercher combien de fois 56 est contenu dans 236.".

a) Détermination du premier chiffre du quotient:

Selon la méthode indiquée, on regarde combien de fois le premier chiffre du diviseur augmenté d'une unité (c'est-à-dire 5+1 = 6) est contenu dans 23. La table de Pythagore donne 3. Le premier chiffre du quotient est donc 3 (pour le moment). On retranche 3 x 56 de 236.

3 x 6 = 18 => on entre 18 sur les roues étoilées en mettant le 8 à l'aplomb du 6 de 56

3 x 5 = 15 => on entre 15 sur les roues étoilées en mettant le 5 à l'aplomb du 5 de 56

Le résultat 6888 apparaît dans les lucarnes, le 56 de la bande de papier étant à l'aplomb du 68. On constate que 56 peut encore être retranché une fois, le premier chiffre du quotient n'est donc pas 3 comme on l'avait noté mais 4.

Le fait de retrancher une fois de plus 56 (il suffit de le rentrer sur les roues étoilées) fait apparaître 1288 à l'afficheur. Le 56 de la bande de papier est à l'aplomb du 12.

Le manuscrit "Usage de la machine" demande à l'opérateur de se munir d'une table de multiplication (appelée "livret", schématisée ci-contre) pour faciliter les opérations. Il précise qu'il est facile de mémoriser cette table. Pour des raisons de facilité de prise de vue, les films qui suivent supposent que l'opérateur connaît sa table de multiplication par cœur.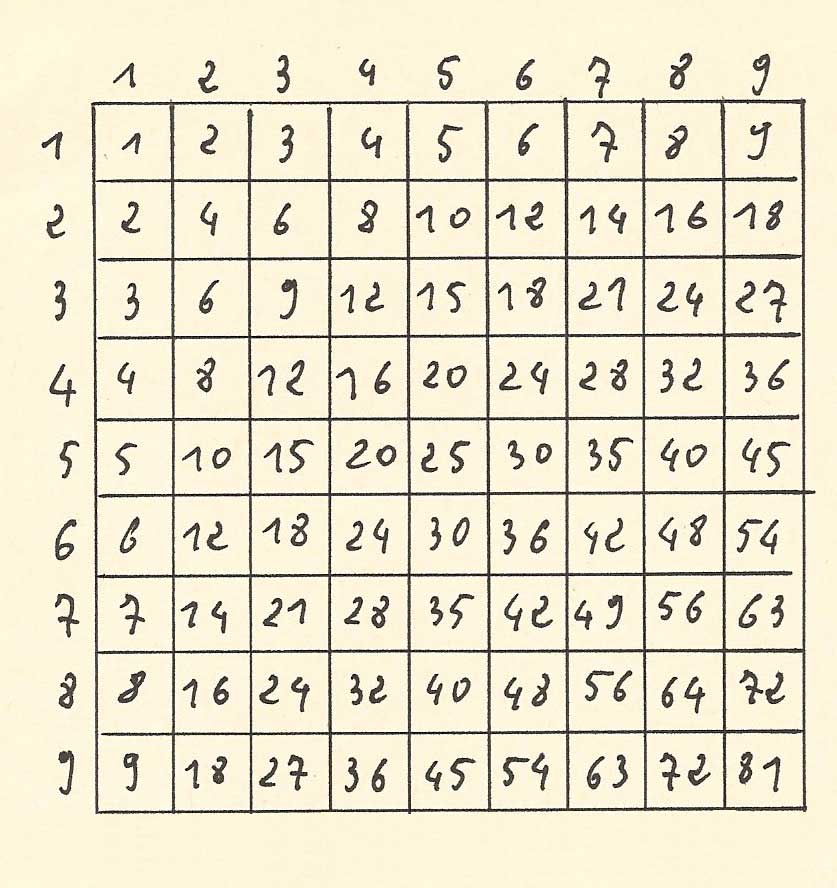

La séquence filmée ci-dessous montre la façon de déterminer le premier chiffre du quotient.

b) Détermination du deuxième chiffre du quotient :

On décale la bande de papier d'une position vers la droite. 56 se trouve maintenant à l'aplomb du 28 de 128. On procède de la même manière.

Combien de fois 6 (5+1) est contenu dans 12. La table de Pythagore donne 2. Le deuxième chiffre du quotient est donc 2 (pour le moment). On retranche 2 x 56 de 128.

2x 6 = 12 => on entre 12 sur les roues étoilées en mettant le 2 à l'aplomb du 6 de 56

2 x 5 = 10 => on entre 10 sur les roues étoilées en mettant le 0 à l'aplomb du 5 de 56

Le résultat 168 apparaît dans les lucarnes, le 56 de la bande de papier étant à l'aplomb du 16. Cette fois, 16 est plus petit que 56 et le second chiffre du quotient n'est pas à modifier.

La séquence filmée montre la suite d'opérations donnant le second chiffre du quotient.

c) Détermination du troisième chiffre du quotient :

On décale la bande de papier d'une position vers la droite. 56 se trouve maintenant à l'aplomb du 68 de 168.

Combien de fois 6 (5+1) est contenu dans 16. La table de Pythagore donne 2. Le troisième chiffre du quotient est donc 2 (pour le moment). On retranche 2 x 56 de 168.

2 x 6 = 12 => on entre 12 sur les roues étoilées en mettant le 2 à l'aplomb du 6 de 56

2 x 5 = 10 => on entre 10 sur les roues étoilées en mettant le 0 à l'aplomb du 5 de 56

56 est affiché dans les lucarnes. On peut soustraire encore une fois ce qui signifie que le troisième chiffre du quotient est à augmenter d'une unité, c'est donc 3. La soustraction supplémentaire donne zéro comme résultat, la division tombe juste.

On a finalement obtenu 23688 / 56 = 423

Le film ci-dessous illustre les étapes conduisant à l'obtention du dernier chiffre du résultat.

La marche à suivre donnée ci-dessus est très détaillée, mais comme on le voit dans les séquences filmées, la technique opératoire est très simple. On en conclut que si la division se faisait de manière moins directe que l'addition, elle était tout à fait abordable (en appliquant la méthode décrite dans le manuscrit du 18ème siècle).