The multiplication with a pascaline

Most of comments we can read (books, articles, internet sites) point out the fact that the Blaise Pascal calculator was essentially an adder. The substraction was more difficult to perform than the addition. As for the multiplication and the division, they was so difficult to do than the pascaline was not usefull for.

The method explained in the manuscript "Usage de la machine" demonstrates that this sentence is too rigid, particularly in case of calculations with decimal numbers.

The multiplication :

The example the author of the manuscript has choosen is the multiplication of 423 by 56.

After saying that it is more convenient to take the largest of these two numbers as multiplicand and the smaller for the multiplicator, it is asked to write the two numbers one over the other on a strip of paper with the same space between the digits as the space that exists between the display windows.

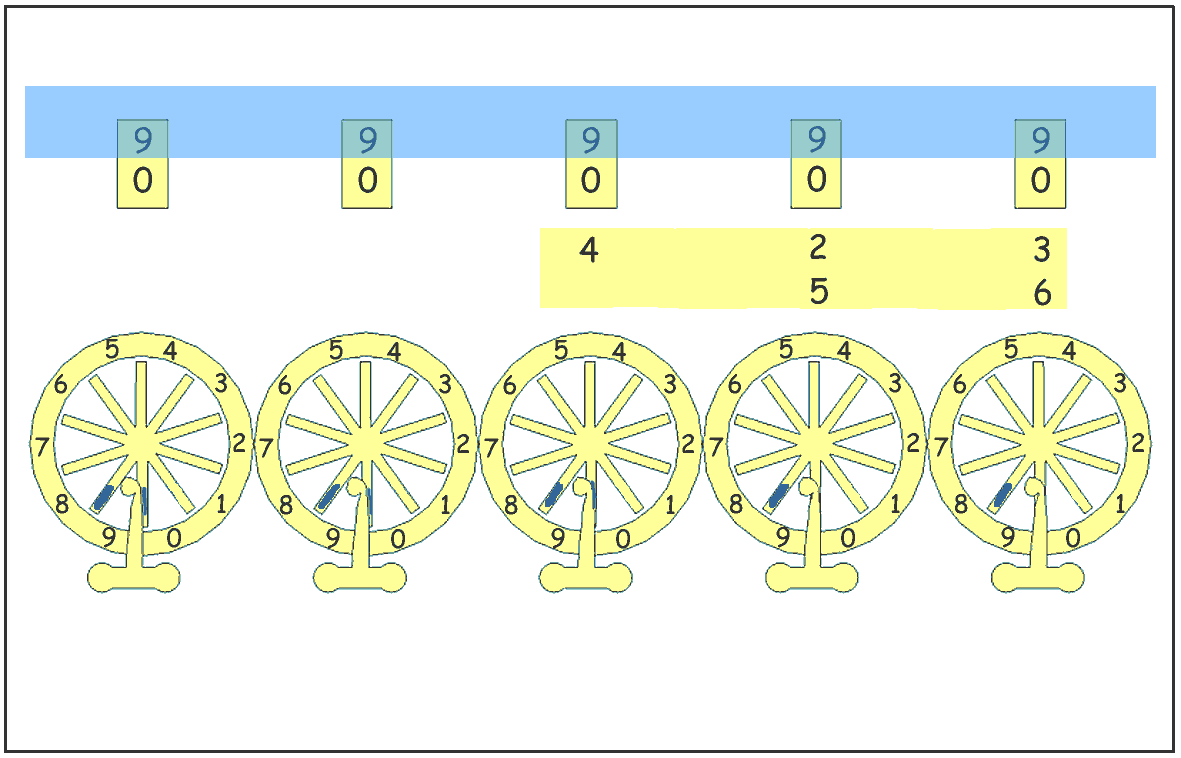1) All the digits of the multiplicand are multiplied one after the other by the unit digit "6" of the multiplicator. For each result of these multiplications, the digit of the unit is set at the same vertical position than the digit of the multiplicand it refers to.

3 times 6 = 18 => one writes 18 setting the "8" at the same position than the "3".

2 times 6 = 12 => one writes 12 setting the "2" at the same position than the "2".

4 times 6 = 24 => one writes 24 setting the "4" at the same position than the "4".

At this step we have performed the multiplication 6 x (400 + 20 + 3)

The manuscript "Usage de la machine" ask the operator to provide itself with a multiplication table (called “booklet”, schematized opposite). It specifies that it is easy to memorize this table. The films which follow suppose that the operator memorized the multiplication table.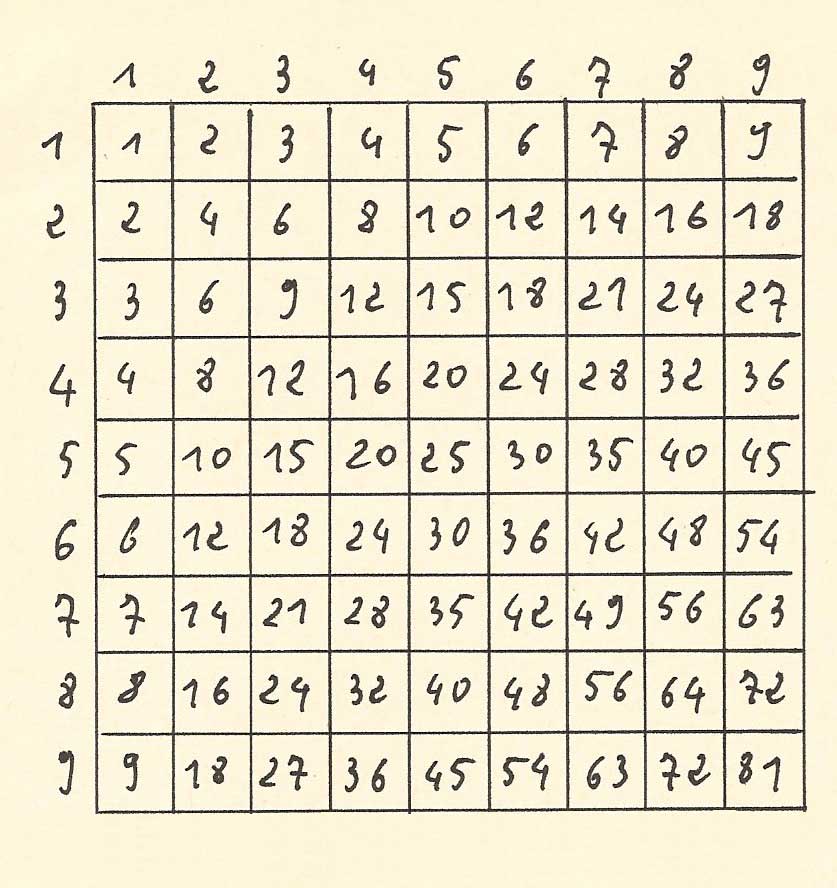

6 x 423 sur la réplique de la pascaline du musée Lecoq de Clermont-Ferrand.

La movie shows the multiplication of 423 by 6 on a reproduction of a pascaline from the Lecoq museum in Clermont-Ferrand.

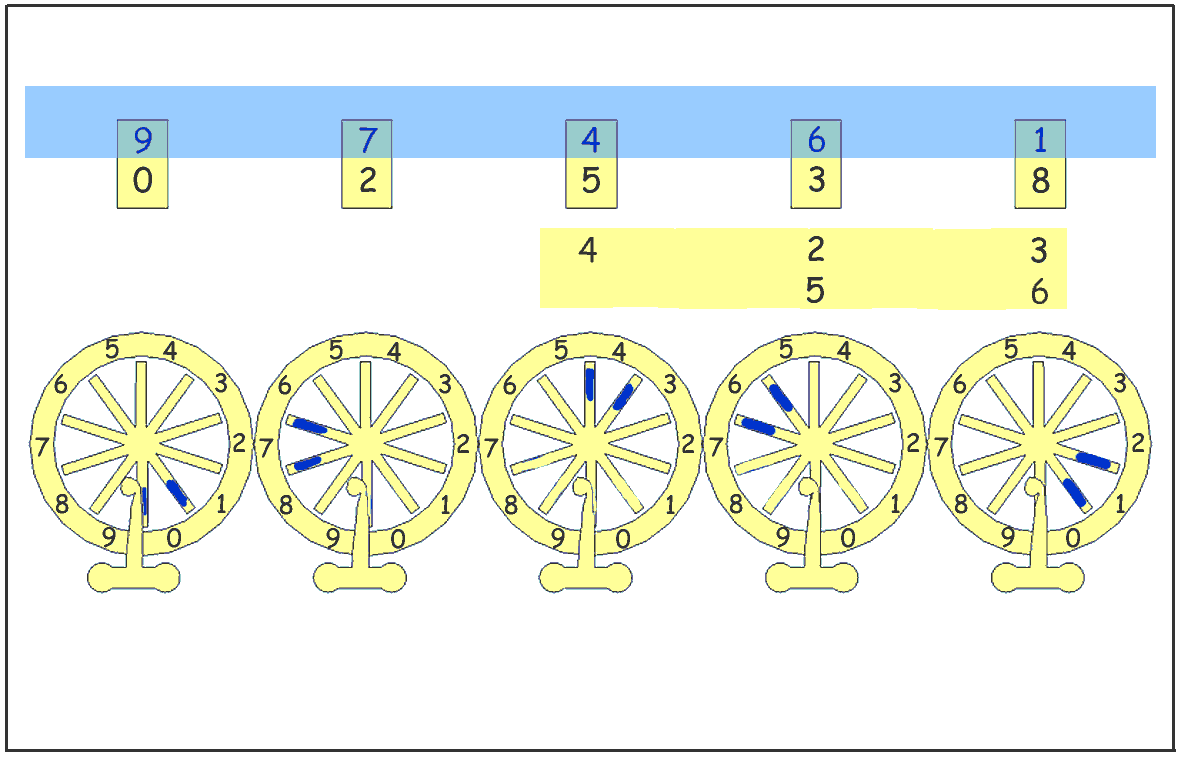
2) To operate with the tens digit "5" of the multiplicator, we shift the strip of paper from one position to the left.

Then we apply the technic as above, that is to say that we perform successively the product of all the digits of the multiplicand by 5. For each result of these multiplications, the digit of the units is vertically aligned with the digit of the multiplicand it refers to.

3 times 5 = 15 => one writes 15 setting the "5" at the same position than the "3".

2 times 5 = 10 => one writes 10 setting the "0" at the same position than the "2".

4 times 5 = 20 => one writes 20 setting the "0" at the same position than the "4".

This succession of operations is illustrated in the following movie.

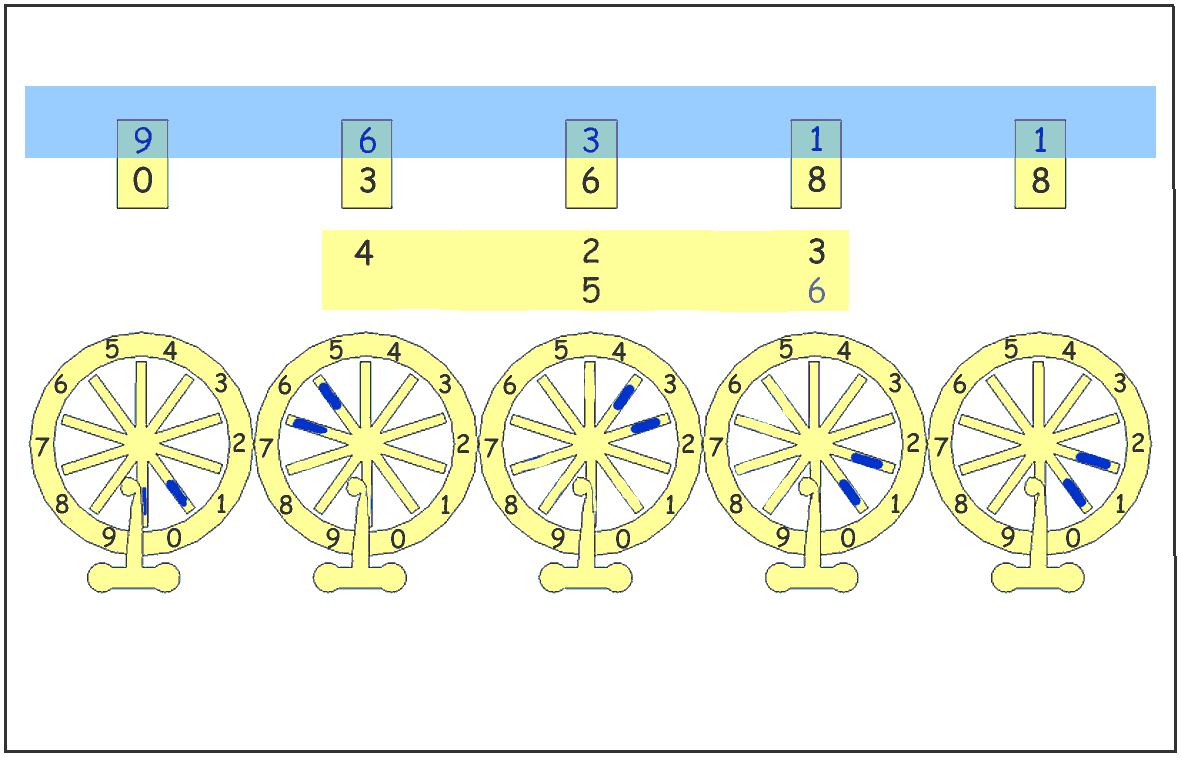
The multiplication is finished, we added the product 5 X (4000 200 30) with the number 2538 which was already in the accumulator. The display windows show the result 23688 which is correct.

This example proves that for the decimal numbers, the multiplication was not so difficult to do that one often claims. Some Troncet adders was equipped with a roll of paper (for example some DA702 models). The user's manual of these adders give a similar method to perform the multiplication.

The manuscript of the 18th century states that a multiplication table is usefull to do the successive multiplications, but that it is not difficult to learn it by heart.

"[...] One must remark than for multiply in such a way the digits of the multiplicand by those of the multiplicator one must use the following table which contains the multiplication of the simple numbers one by each other and which is usually called the "livret". It is easy to learn and to be familiarized with this table in such a way that one does not need to refer to it to perform the calculations".